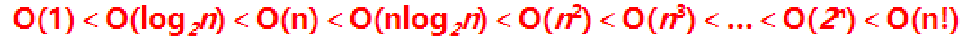先决条件

  • 一般来说，一个算法执行所消耗的时间从理论上是算不出来的。
  • 一个算法花费的时间与算法中语句的执行次数是成正比的。
  • 哪个算法语句执行次数多，它花费的时间就多。

概念

  1. 对于算法最重要的是数量级和趋势，这些是分析算法主要的部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。
  2. 时间复杂度实际上就是一个函数，该函数计算的是执行基本操作的次数。一个算法语句总的执行次数是关于问题规模N的某个函数，记为f(N），N称为问题的规模。语句总的执行次数，记为T[N]，当N不断变化时，T[N]也在不断变化，算法的执行次数的增长速率和f(N)的增长速率相同。则T[N]=O(f(N)),称O(f(N))为时间复杂度的O渐进表示法。

分类

  • 算法完成工作最少需要多少基本操作叫做最优时间复杂度，是一种最乐观最理想的状态。
  • 算法完成工作最多需要多少基本操作叫做最坏时间复杂度，是算法的一个保障。
  • 算法完成工作平均需要多少基本操作叫做平均时间复杂度，它可以均匀全面的评价一个算法的好坏。

计算规则

  1. 基本操作,即只有常数项，认为其时间复杂度为O(1)
  2. 顺序结构，时间复杂度按加法进行计算
  3. 循环结构，时间复杂度按乘法进行计算
  4. 分支结构，时间复杂度取最大值
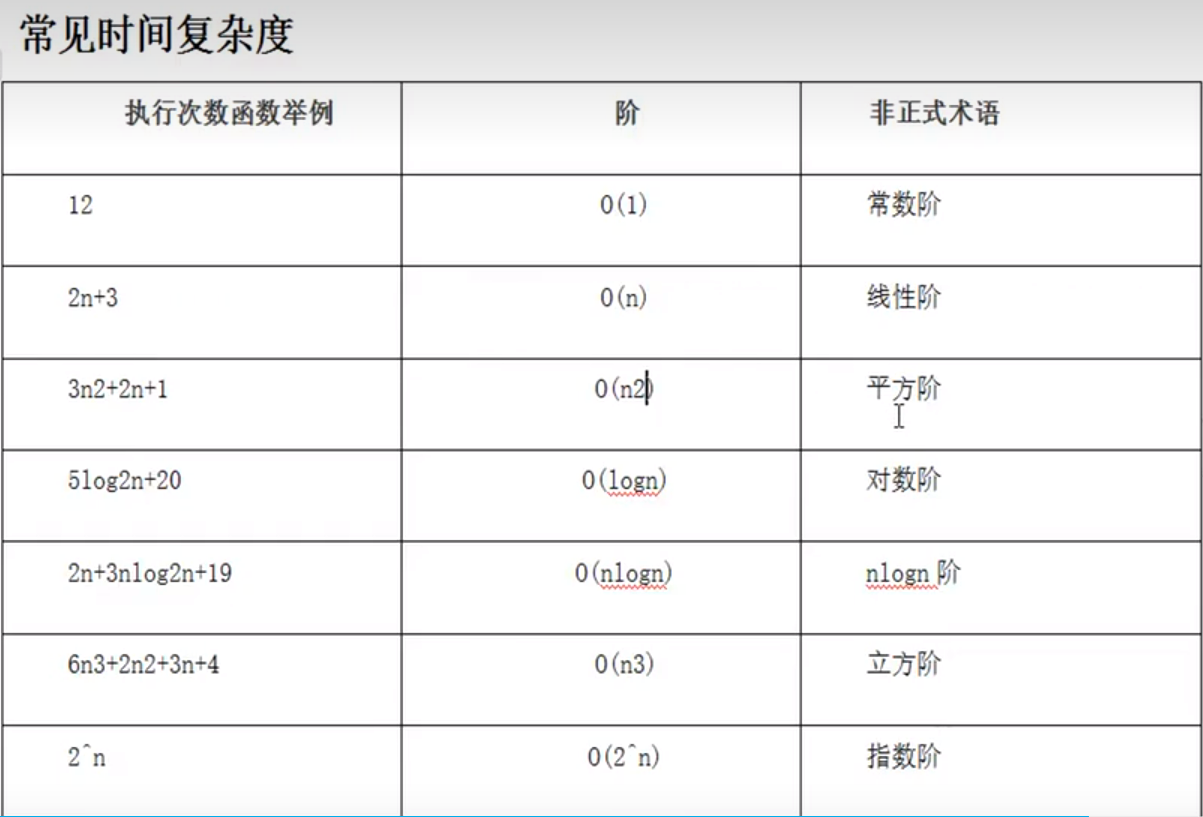
  5. 判断一个算法效率时，往往只需要关注操作数量的最高次项，其他次要项和常数项可以忽略
  6. 在没有特殊说明时，我们所分析的时间复杂度都是指最坏时间复杂度

案例分析

见csdn博客：
详解时间复杂度计算公式(附例题细致讲解过程)：

https://blog.csdn.net/weixin_63866037/article/details/128087397

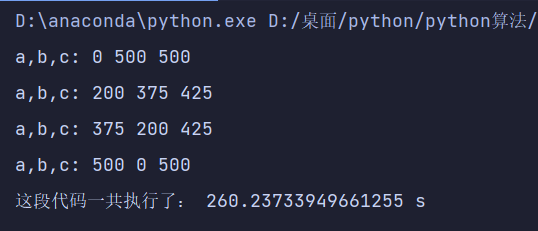
没学算法前：三次暴力循环

1
2
3
4
5
6
7
8
9
import time
begin_time = time.time()
for a in range(0,1001):
    for b in range(0,1001):
        for c in range(0,1001):
            if a+b+c == 1000 and a**2+b**2 == c**2:
                print("a,b,c:",a,b,c)
end_time = time.time()
print("这段代码一共执行了：",end_time-begin_time,"s")

image.png
时间复杂度为O(n^3)
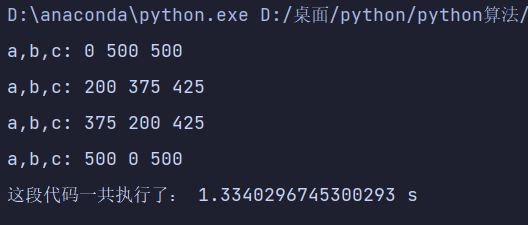
学过算法之后：通过abc关系直接生成c：

1
2
3
4
5
6
7
8
9
import time
begin_time = time.time()
for a in range(0,1001):
    for b in range(0,1001):
        c = 1000-a-b
        if a+b+c == 1000 and a**2+b**2 == c**2:
            print("a,b,c:",a,b,c)
end_time = time.time()
print("这段代码一共执行了：",end_time-begin_time,"s")

image.png
时间复杂度为O(n^2)
image.png
image.png