概念

二叉树是每个节点最多有两个子树的树结构。通常子树被称作”左子树“（left subtree)和”右子树“（right subtree)。

性质

  1. 在二叉树的第i层上至多有2^(i-1)个节点(i>0)
  2. 深度为k的二叉树至多有2^k-1个节点
  3. 对于任意一颗二叉树，如果其叶节点数为N0，而度数为2 的节点总书为N2，那么N0 = N2+1
  4. 具有n个系欸点的完全二叉树的深度必为log2(n+1)
  5. 对完全二叉树 ，若从上到下、从左到右编号，则编号为i的结点，其左孩子编号必为2i，其右孩子编号必为2i+1；其双氢的编号必为i/2 （i=1时为根除外）

特殊二叉树

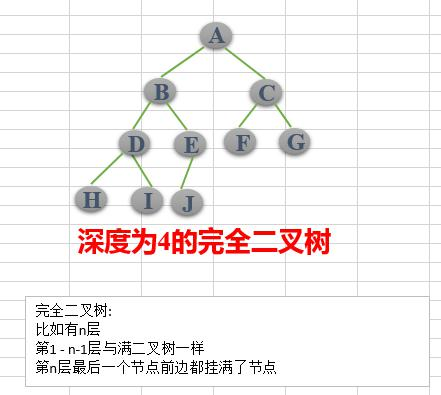
完全二叉树：设二叉树的高度为h，除第h层外，其他各层（1~h-1）的节点数都达到最大个数，第h层有叶子节点，并且叶子节点都是从左到右依次排布，这就是完全二叉树。
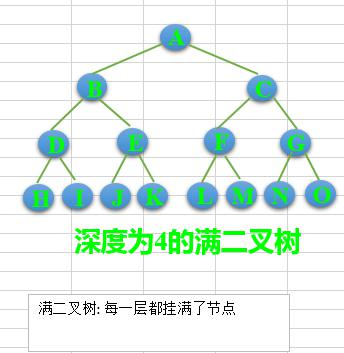
image.png
满二叉树：除了叶节点外每个节点都有左右子叶且叶子节点都处在最外层的二叉树
image.png

二叉树的节点及树的创建

  1. 节点创建

    1
    2
    3
    4
    5
    class Node(object):
        def __init__(self,elem=-1,lchild=None,rchild=None):
            self.elem = elem
            self.lchild = lchild
            self.rchild = rchild

  2. 树的初始化

    1
    2
    3
    4
    class Tree(object):
        def __init__(self,root = None):
            self.root =root

  3. 添加节点

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    def add(self,elem):
        # 首先创建节点
        node = Node(elem)
        # 如果树是空的，则对root根赋值
        if self.root == None:
            self.root = node
        else:
            queue = []
            queue.append(self.root)
            # 对已有的节点进行层次遍历
            while queue:
                cur = queue.pop(0)
                if cur.lchild == None:
                    cur.lchild = node
                    return
                elif cur.rchild == None:
                    cur.rchild = node
                    return
                else:
                    #如果左右子树都不为空，加入队列继续判断
                    queue.append(cur.lchild)
                    queue.append(cur.rchild)